6. 计算正确性
在本章中, 我们将简述完全正确性和部分正确性的概念, 并介绍霍尔逻辑和正确性的证明方法.
完全正确性和部分正确性
在描述程序的正确性时, 我们首先需要明确前提条件和对程序的期望, 只有在这一基础上才能对程序是否具备正确性做出判断. 回顾第四章所介绍的定义, 我们认为程序是操纵状态的函数, 也就是说, 程序接收一个初始状态, 并将其变换为某个截止状态. 程序 $P$ 的实际行为可以表示为:
\[\text{Actual}(P) \equiv \{<\sigma_{start}, \sigma_{end}> ~\vert~ <P, \sigma_{start}> \Rightarrow \sigma_{end}\}\]而我们可以使用两个 谓词 描述程序的理想行为: $\text{Pre}$ 表示起始状态, 而 $\text{Post}$ 表示终止状态. 在此处, 我们假设只关心程序在满足起始状态的条件下运行所会发生的情况如何. 这样的理想行为可以描述为
\[\text{Specification}(\text{Pre}, \text{Post}) \equiv \{<\sigma_{start}, \sigma_{end}> ~\vert~ <\text{Pre}(\sigma_{start}) \Rightarrow \text{Post}(\sigma_{end})\}.\]而我们对程序正确性的判断即是对
\[\text{Specification}(\text{Pre}, \text{Post}) \subseteq \text{Actual}(P).\]是否成立的判断.
上述的, 对程序正确性的描述存在几个问题: 首先, 这一描述是粗略而不严谨的. 其次, 该描述仅适用于会在有限步内终止的程序, 而不适用于死循环.
若我们不考虑程序永不终止的情况, 即使在某些初始条件下程序始终都不会终止也没关系, 则我们所考虑的正确性即被称为 部分正确性, 反之则是 完全正确性.
严格上来说, 检查程序是否在终止时满足条件的问题是检查程序部分正确性的问题. 检查程序是否满足其规范并且要求程序始终会终止的问题称为对程序的完全正确性的检验.
在描述程序正确性时, 一个难题是确定 While 循环的正确性. 由于我们难以确定 While 的循环次数, 因此执行循环前的状态和循环后的状态之间难以建立确定的联系. 为了解决这一问题, 我们引入 循环不变量 的概念:
定义: 循环不变量
程序段 \(\text{while} ~b~ \text{do} ~S~\) 的 循环不变量 是一个每次循环体 $S$ 执行前后都恒为真的谓词 $P$.
注意: 它在循环体执行过程中的真伪并不是我们所关心的.
我们下面介绍描述程序的 部分正确性 的公理系统:
霍尔逻辑: 描述部分正确性
定义: 霍尔三元组
部分正确性的霍尔三元组 (
Hoare Triple) 是由两个谓词和一个陈述组成的, 记为: \(\{P\} ~S~ \{Q\}\) 并且我们规定 $P, Q$ 分别为陈述 $S$ 的 前置条件 和 后置条件.
若某个霍尔三元组是合法的 (Valid), 则程序在前置条件下开始执行, 要么永远不会停止, 要么程序终止时所处的状态恰好为后置条件. (即满足部分正确性)
要使用霍尔三元组检查给定程序的部分正确性, 我们将引入一系列规则, 并利用这些规则将程序分割成多条指令, 并对这些指令一一检查.
下面我们介绍使用霍尔三元组检查程序部分正确性的推断规则:

霍尔逻辑: 描述完全正确性
在使用霍尔三元组描述程序的完全正确性时, 我们需要对表示符号作简要修改, 并使用新的 $\text{while}$ 规则替换部分正确性中的推断规则:
定义: 霍尔三元组
部分正确性的霍尔三元组 (
Hoare Triple) 是由两个谓词和一个陈述组成的, 记为: \([P] ~S~ [Q]\) 并且我们规定 $P, Q$ 分别为陈述 $S$ 的 前置条件 和 后置条件.
在考虑程序的完全正确性时, 我们要确保循环体总是能在有限步内终止. 为了检测这一点, 我们使用如下的 $\text{while}$ 规则:
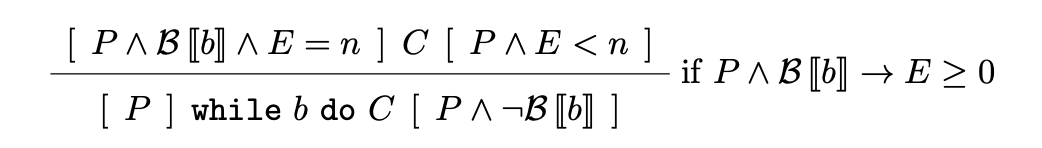
其中, $E$ 为一个随着循环执行而递减且其值恒有下界的表达式. 由此, 若某个霍尔三元组满足条件, 则可确定它所表示的是一个一定能在有限步内终止的循环.
正确性证明的技巧及方法
程序正确性的证明具有一定的技巧性, 其原因在于我们无法直接地判断任何给定程序的正确性, 因而也就没有某种通用算法. 然而, 证明流程中仅仅在: 1. 构造/寻找/生成 循环不变量 2. 应用 $\text{cons}$(Consequence) 规则将某个三元组转换为与之等价的另一个三元组 这两个部分中存在较高的技巧性, 而其余的步骤基本上是机械性的赋值, 转换和联结.
一般地:
考虑形如
\[S_1; ~ (\text{while} ~ b ~\text{do}~ S_2); ~ S_3\]的程序, 假定其前置条件和后置条件分别为 $P, Q$:
不难观察到程序中存在循环体结构 $\text{while}$, 并且程序被分为 前部程序体 循环体 后部程序体 三个部分.
- 首先, 寻找或构造出循环体的循环不变量 $R$. 并使用基本规则推导
和
\[\{R \wedge \neg b\} ~ S_1 ~ \{Q\}.\]若无法证明, 则说明所找到的循环不变量不够强, 需要将循环不变量所包含的条件进一步强化后再试.
- 在得到 前部程序体 和 后部程序体 这两个部分的正确性证明后, 我们对循环体
给出证明.
- 最后, 对表示循环体的霍尔三元组应用 $\text{while}$ 规则, 再使用 $\text{comp}$ 规则将三者联结起来, 证毕.
需要注意的是, 循环体的循环不变量不一定存在. 但可以确定的是, 循环不变量必须满足以下条件:
- 循环不变量必须包含所有循环体在循环中更新 并在循环主体之后或在后置条件中引用的变量.
- 我们所希望在循环结束后仍然为真的条件必须包含在循环不变量中.
- 循环不变量中需要包含程序中所使用的常量.
- 后置条件的形式往往和循环不变量保持一致. 比如: 若后置条件是一个不等式, 我们可以尝试将后置条件这个不等式直接作为循环不变量.
- 循环不变量的真伪不会被循环体的执行与否而改变.