可满足性检验
从本章起我们将循序渐进地对 可满足性检验 问题展开介绍和讨论. 首先我们明确 可满足性检验问题 的概念:
定义 4.0.1 (可满足性问题)
考虑一个以由有限个谓词公式组成的集合作为 实例 的决策问题, 若这个由谓词公式组成的集合是 可满足的, 则该决策问题的实例的答复为肯定的.
可满足性问题和数学中的定理证明有着非常紧密的联系. 数学上, 一个定理一般表现为下列形式:
给定公理/定理 $A_1, A_2, \cdots, A_n$, 求证公式(也就是我们的推测) $G$.
在数理逻辑中, 从 $A_1, A_2, \cdots, A_n$ 中证明 $G$ 实际上等价于检查 $A_1 \wedge A_2 \wedge \cdots \wedge A_n \rightarrow G$ 的正确性, 而这个正确性检查问题又可以被归结于检查公式集合 ${A_1, \cdots, A_n, \neg G}$ 是否为不可满足的.
4.1 真值表
最简单的可满足性检查方式是在一张表中列出给定谓词公式所有可能的解释, 并依次检查公式在这些解释下是否出现了不可满足的情况. 为了方便求值, 我们一般会将公式拆分为最小的子公式 (subformula). 一张典型的真值表如图:

值得注意的是, 我们很快就能发现, 在某些情况下我们可以利用逻辑运算符的短路特性, 只需检查部分的几个谓词变量的值即可判断整个谓词表达式的可满足性.
4.2 分割法
分割法在语义上和真值表等价. 它的基本原理是, 遍历地为给定的谓词公式中的变量分别赋值, 并在每一次赋值后基于一套规则利用逻辑运算符的短路特性和等价代换性质简化公式.
引理 4.2.1
记谓词公式 $A$, 谓词原子 $p$ 和解释 $I$. 则有:
若 $T \vDash \neg p$, 则 $A$ 在解释 $I$ 中和 $A_{p}^{\perp}$ 等价.
若 $T \vDash p$, 则 $A$ 在解释 $I$ 中和 $A_{p}^{\top}$ 等价.
证明
考虑情形 $2$, 情形 $1$ 同理. 由 $T \vDash p$ 可知 $I \vDash T \leftrightarrow p$. 由等价代换定理可得: $I \vDash A \leftrightarrow A_{p}^{\top}$, 故有 $I \vDash A$ 当且仅当 $I \vDash A_{p}^{\top}. ~ \blacksquare$
定理 4.2.1
记谓词公式 $A$ 和谓词原子 $p$, 则 $A$ 为可满足的, 当且仅当 $A^{\top}{p}$ 和 $A^{\perp}{p}$ 中至少有一个为可满足的.
证明
必要性: 不妨假设 $A$ 为可满足的, 则存在解释 $I$ 使 $I \vDash A$. 考虑 $I \vDash p$ 的情形, 由上述引理可得 $I \vDash A \leftrightarrow A_{p}^{\top}$. 因此有 $I \vDash A_{p}^{\top}$, 也就是 $I \vDash A_{p}^{\top}$ 为可满足的.
充分性: 考虑 $A_{p}^{\top}$ 可满足的情形. 则存在解释 $I$, 使 $I \vDash A_{p}^{\top}$ 成立. 如下定义解释 $I’$:
\[I'(q) \overset{\text{def}}{=} \begin{cases} I(q) ~~~ \text{if} ~ p \neq q \\ 1~~~~~~~~\text{if} ~ p=q \end{cases}\]由此可得 $I’ \vDash A_{p}^{\top}$. 由于我们有 $I \vDash p$, 故由上述引理可得 $I’ \vDash A \leftrightarrow A_{p}^{\top}$. 因此 $I’ \vDash A$, 可知 $A$ 为可满足的. $\blacksquare$
上述定理的结论可以被可满足性算法如此应用:
算法首先选定一个在公式 $G$ 中出现的谓词变量 $p$, 检查是否 $G_{p}^{\top}$, $G_{p}^{\perp}$ 中至少有一个公式为可满足的. 这样, 原问题被 分割 为两个子问题. 此外, 在执行分割时我们还可将 $G_{p}^{\top}$, $G_{p}^{\perp}$ 使用 覆写规则 (rewrite rule) 简化, 如果这可能的话.
在正式介绍 分割算法 前, 我们需要再引入一个定义.
定义 4.2.1 (有符号公式)
称形为 $A = b$, 其中 $A$, $b$ 分别为谓词公式和布尔值的表达式为 有符号公式.
若解释 $I$ 满足 $I(A)=b$, 可知 $I \vDash A=b$, 也就是公式在该解释下为真, 则称 $I$ 为公式 $A=b$ 的一个模型. 有符号公式为 可满足的, 若它有一个对应的模型.
我们不难从定义中得到下列性质:
-
对任意公式 $A$ 和解释 $I$, $A=1$ 和 $A=0$ 中恰有一个为真.
-
公式 $A$ 为可满足的, 当且仅当有符号公式 $A=1$ 为可满足的.
算法 4.2.1 (分割算法)
分割算法以公式 $G$ 为输入, 其输出值为 satisfiable 或 unsatisfiable. 我们同时将从 $G$ 中选择一个有符号原子 $p=b$ 的操作参数化为 select_signed_atom.
若所选择的有符号原子为 $p=1$, 算法首先在 $p$ 为真的情况下尝试对 $G$ 建模. 若不能找到这样的解释, 它再转而考虑 $p$ 为假的情形, 反之亦然.

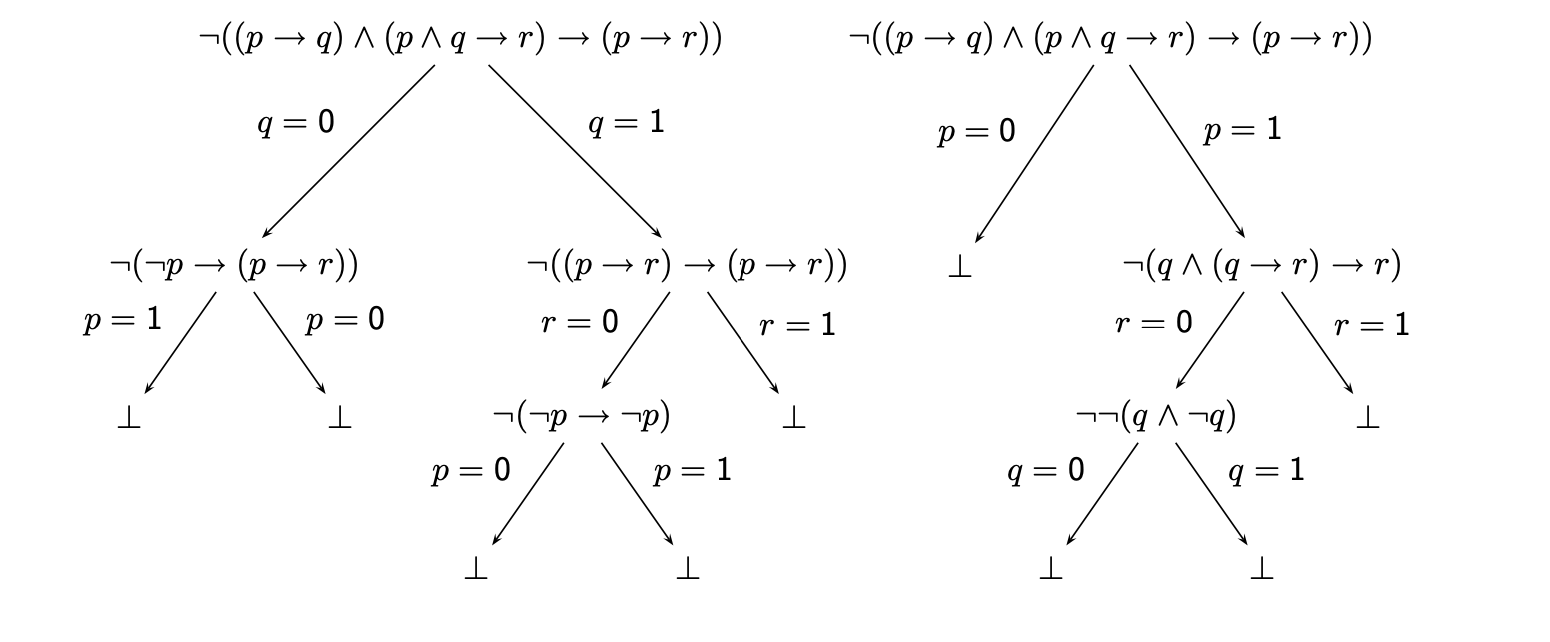
算法的执行过程可以被可视化为一棵 分割树. 它的节点为算法处于不同步骤时待处理的谓词公式 $G$, 它的边被所选择的有符号谓词原子标记.
不难看出, 分割树的大小受对有符号原子公式的选择影响, 且对原子公式的选择顺序也会影响分割树的大小.
定理 4.2.2
分割算法是一种可靠, 完备且必会在有限步内终止的算法:
- 若给定的公式 $G$ 为可满足的, 则分割算法会终止并返回结果
satisfiable.- 若给定的公式 $G$ 为不可满足的, 则分割算法会终止并返回结果
unsatisfiable.
4.3 子公式的极性
本节我们将引入 极性 的概念, 并利用这一概念执行对谓词公式的可满足性检验算法的优化.
我们下面引入面向真值 $1, 0$ 的偏序 $<$, 其中有 $0 < 1$. 该偏序同时使
\[0 \leqslant 0, ~ 0 \leqslant 1, ~ 1 \leqslant 0,~ 1 !\leqslant 0.\]定义 4.3.1 (单调和非单调函数)
给定函数 $f(x_1, \cdots, x_n)$ 和整数 $k$, $1 \leqslant k \leqslant n$. 称 $f$ 在它的第 $k$ 个参数上单调, 若对于 $v_1, \cdots, v_n, v’_{k}$, 我们有
\[f(v_1, \cdots, v_k, \cdots, v_n) \leqslant f(v_1, \cdots, v'_k, \cdots, v_n)\]若 $v_k \leqslant v’_k$, 反之称其为 非单调的.
由于逻辑联结词同样可被视为布尔函数, 我们相应地考察它们的单调性不难发现, 对于任何位置上的变量, 连接词 $\vee, ~ \wedge$ 均为 单调的; $\neg$ 为非单调的, $\rightarrow$ 对于它的第二个变量单调, 而对于第一个变量非单调. $\leftrightarrow$ 则对它的任一元素既不单调也不非单调.
极性可被视为对谓词公式的布尔值与其子公式布尔值之间关系的描述. 利用谓词公式 (函数) 的单调性, 我们可以在已知它的某个子式值的前提下对它本身的值进行推测.
定义 4.3.2 (位置和极性)
称 位置 为一列顺序随机的整数 $a_1, a_2, \cdots. a_n$, 其中 $n \geqslant 0$, 写为 $a_1.a_2. \cdots .a_n$.
$n=0$ 时序列为空, 我们称其为 空位置, 记为 $\epsilon$. 极性 为一个可取 $-1, 0, 1$ 的值.
下面我们分别递归地定义:
- 给定公式中的位置
- 位于公式 $A$ 的位置 $\pi$ 处的子公式 $A\vert_{\pi}$
- 位于公式 $A$ 的位置 $\pi$ 处的子公式 $A\vert_{\pi}$ 的极性 $\text{pol}(A, \pi)$
i. 对任何公式 $A$, $\epsilon$ 为 $A$ 中的一个位置, 且有
\[A\vert_{\epsilon} \overset{\text{def}}{=} A, ~ \text{pol}(A, \pi) = 1.\]
ii. 令 $A\vert_{\pi} = B$:
若子公式 $B$ 形如 $B_1, \wedge \cdots \wedge B_n$ 或 $B_1, \vee \cdots \vee B_n$, 则对 $\forall ~ i \in [n]$: 位置 $\pi.i$ 位于 $A$ 中, $A \vert_{\pi.i} \overset{\text{def}}{=} B_i$, 且有 $\text{pol}(A, \pi.i) \overset{\text{def}}{=} \text{pol}(A, \pi)$.
若子公式 $B$ 形如 $\neg B_1$, 则 $\pi.1$ 为 $A$ 中的一个位置, $A\vert_{\pi.1} \overset{\text{def}}{=} B_1$, 且有 $\text{pol}(A, \pi.1) \overset{\text{def}}{=} -\text{pol}(A, \pi)$.
若子公式 $B$ 形如 $B_1 \rightarrow B_2$, 则 $\pi.1, \pi.2$ 为 $A$ 中的一个位置, $A\vert_{\pi.1} \overset{\text{def}}{=} B_1$, $A\vert_{\pi.2} \overset{\text{def}}{=} B_2$, 且有 $\text{pol}(A, \pi.1) \overset{\text{def}}{=} -\text{pol}(A, \pi)$, $\text{pol}(A, \pi.2) \overset{\text{def}}{=} \text{pol}(A, \pi)$.
若子公式 $B$ 形如 $B_1 \leftrightarrow B_2$, 则 $\pi.1, \pi.2$ 为 $A$ 中的一个位置, $A\vert_{\pi.1} \overset{\text{def}}{=} B_1$, $A\vert_{\pi.2} \overset{\text{def}}{=} B_2$, 且有 $\text{pol}(A, \pi.1) \overset{\text{def}}{=} \text{pol}(A, \pi.2) =0$.
若 $A\vert_{\pi} = B$, 同时称 $B$ 在 $A$ 的位置 $\pi$ 处出现. 若 $\text{pol}(A, \pi) = 1$ (或 $0$), 则称 该位置上的 $B$ 为正出现实例 (Positive Occurrence) (或负出现实例).
我们同样可以使用 生成树 可视化给定公式的位置和对应位置上子式的极性. 不难看出:
-
若子公式 $B$ 在逻辑运算符 $\leftrightarrow$ 的任一个域 (也就是左边或右边) 出现, 则位置$\pi$ 的极性为 $0$.
-
若子公式 $B$ 不在逻辑运算符 $\leftrightarrow$ 的任一个域 (也就是左边或右边) 出现, 则位置$\pi$ 的极性为 $1$ (相应地, $-1$). 当且仅当 $B$ 在逻辑运算符 $\neg$ 的域中出现, 或在运算符 $\rightarrow$ 的左侧域中出现了偶数次 (相应地, 奇数次).
极性 的一个主要性质即为, 它实质上为我们提供了 单调性 的一个语义上等价的表示法. 举例而言, 性质
\[I(A) \leqslant I(B)\]即可被表示为
\[I \vDash A \rightarrow B.\]引理 4.3.1 (单调替换)
记 $A, B, B‘$ 为谓词公式, $I$ 为一个解释, 且满足 $I \vDash B \rightarrow B’$. 若
\[\text{pol}(A, \pi) = 1,\]则有
\[I \vDash A[B]_{\pi} \rightarrow A[B']_{\pi}.\]相应地, 若
\[\text{pol}(A, \pi) = -1,\]则有
\[I \vDash A[B']_{\pi} \rightarrow A[B]_{\pi}.\]
该引理的结论同时蕴含了下述定理:
定理 4.3.1(单调替换)
记 $A, B, B‘$ 为谓词公式, 满足 $B \rightarrow B’$ (相应地, 满足 $B‘ \rightarrow B$).
记由替换公式 $A$ 中至少一个 $B$ 的 正出现实例 (相应地, 负出现实例) 所得到的公式为 $A‘$, 则 $A \rightarrow A’$ 为真.
将上述定理所描述的性质用 可满足性 的语言重新叙述, 就得到了下列推论:
推论 4.3.1
记 $A, B, B‘$ 为谓词公式, $B \rightarrow B’$ 为真 (相应地, $B‘ \rightarrow B$ 为真).
记由替换公式 $A$ 中至少一个 $B$ 的 正出现实例 (相应地, 负出现实例) 所得到的公式为 $A‘$, 若 $A$ 为可满足的, 则 $A’$ 也是可满足的.
在谓词公式的可满足性检测问题中, 极性 的定义起到了重要的作用. 称 谓词原子 $p$ 在谓词公式 $A$ 中是纯粹的, 若它在 $A$ 中所有的出现实例都是正的或都是负的.
引理 4.3.2 (纯粹原子)
记 $p$ 为一个在 $A$ 中是纯粹的原子, 取 $A$ 的一个解释 $I$, 则解释 $I‘$ 可通过下述步骤生成:
\[I'(q) \overset{\text{def}}{=} \begin{cases} 1, ~~~~~~~\text{if} ~ p=q~ \text{and} ~p~ \text{occurrs in}~A~\text{only positively.}\\ 0, ~~~~~~~ \text{if} ~ p=q~ \text{and} ~p~ \text{occurrs in}~A~\text{only negatively.} \\ I(q)~~~~ \text{if}~p \neq q.\end{cases}\]
证明
下面只考虑 $A$ 中 $p$ 的所有出现实例 均为正 的情形. 首先可得 $p \rightarrow \top$ 为重言式. 由 单调替换定理: $A \rightarrow A_{p}^{\top}$ 亦为重言式.
由 $I \vDash A$, 相应的有 $I \vDash A_{p}^{\top}$. 由于 $p$ 不在 $A_{p}^{\top}$ 中出现且 $I$ 和 $I‘$ 对于任何不为 $p$ 的变量的解释均相同, 故有 $I’ \vDash A_{p}^{\top}$.
同时, 由 $I’$ 的构造可知它满足 $I’ \vDash p \leftrightarrow \top$, 故由 等价替换定理 可得 $I’ \vDash A.~\blacksquare$
我们下面再给出一个描述与上述引理等价的定理:
定理 4.3.2 (纯粹原子)
记原子 $p$ 在 $A$ 中有且只有正出现实例 (或负出现实例). 则 $A$ 为可满足的, 当且仅当
\[A^{\top}_{p} ~~ (A^{\perp}_{p})\]为可满足的.
证明
必要性: 由 $p \rightarrow \top$ 为重言式, 由单调替换定理
也是重言式, 因此 $A$ 的任何模型都是 $A^{\top}_{p}$ 的 $. ~ \blacksquare$
充分性: 记 $A^{\top}_{p}$ 的一个模型 $I$.
将它对变量 $p$ 的解释重定义, 使得 $I’(p)=1$. 则此时 $I’$ 还是 $A^{\top}_{p}$ 的一个模型, 但此时同时有
\[I' \vDash p \leftrightarrow \top.\]故由等价替换定理: $I’ \vDash A \leftrightarrow A^{\top}_{p}$, 因而 $I’ \vDash A$, 进而 $A$ 是可满足的. $\blacksquare$
显然, 纯粹原子定理可有效地应用于对分割算法的优化: 给定谓词公式 $G$, 若 $p$ 在 $G$ 中是 纯粹的, 则依照其极性我们将 $G$ 中的所有 $p$ 替换为 $G_{p}^{\top}$ 或 $G_{p}^{\perp}$, 因而可以避免任何对 $p$ 的分割, 从而简化了算法的执行步骤.
