约束满足问题

在本章中, 我们将解释 约束满足问题 的定义和对它的建模方式, 并将其形式化为搜索问题.

1. 对约束满足问题的定义和建模

定义 1.1 (约束满足问题)

我们称 要求我们针对 给定的一组变量 以及这些变量的 需要满足的一些限制和约束条件, 找出 符合这些所有限制条件 的解的问题为 约束满足问题 (Constraint Satisfaction Problem), 又称 约束满足网络 (Constraint Satisfaction Network).

形式上, 约束满足问题为一个三元组 $\mathcal{N} = \langle \bar{x}, \bar{D}, C\rangle$, 其中:

1. $\bar{x}$ 为 变量集合 ${x_1, \cdots, x_n}.$
2. $\bar{D}$ 为 值域集合 ${D_1, \cdots, D_n}$, 每个 $D_i$ 分别对应值域集合中的 $x_i$.

3. $C$ 为描述变量取值的 约束集合:
   $C$ 中的每个元素均为有序对

   \[\langle \text{scope}, \text{relation}\rangle\]

   其中 $\text{scope}$ 为约束中的变量组 (若只涉及两个变量就是变量对), $\text{relation}$ 为变量组中涉及的变量 需要满足的关系.

   如考虑变量 $X_1, X_2$, 要求它们必须满足关系 $X_1 \neq X_2$, 则可以将该约束表示为这样的有序对:

   \[\langle(X_1, X_2), X_1 \neq X_2\rangle.\]

   除了表示为抽象关系之外, 约束也可以表示为对所有关系元组的列举.

我们下面定义 状态空间 和 解 的概念:

定义 1.2 (状态空间)

称由 状态 组成的集合为给定问题的 状态空间. 状态 为对部分或全体变量的一个 赋值.

定义 1.3 (赋值的相容性与完整性)

若某个赋值 不违反任何约束条件, 则称其为 相容的, 也称为 合法的.

若某个赋值中, 所有的变量均被赋值, 则称其为 完整赋值. 反之, 则称为 部分赋值.

定义 1.4 (约束满足问题的解)

称某个问题的任何 相容且完整 的赋值为该问题的解.

定义 1.5 (约束)

称只限制单个变量取值的约束为 一元约束, 与两个变量相关的约束为 二元约束.

违反直觉的是, 变量个数任意 的约束称为 全局约束 (但它不一定涉及问题中的所有变量). 要求约束中的所有变量取值必须互异的约束 Alldiff 就是一种全局约束.

若我们考虑约束中变量可取值的范围, 就会对问题的难易程度和处理方式产生直接影响.

最简单的 CSP 问题涉及的变量是 离散且值域有限 的, 若值域无限, 则我们只能使用 约束语言 而非像有限值域情形下那样枚举受约束变量的所有可能取值. 我们在这里暂不考虑值域无限的情形.

2. 约束传播 (Constraint Propogation)

在上一章中, 我们已经介绍了数种常见的可用于解决一些问题的状态空间搜索算法. 这些算法唯一能执行的操作只有搜索, 而在 CSP 中, 除了搜索之外算法还可以执行称为 约束传播 的逻辑推理. 由于在约束满足问题中, 对于一些变量的取值存在关系上的约束, 我们可以在利用这些约束来排除某些变量的非法取值, 缩小它的取值范围, 并进一步根据变量间的关系推断其他变量的取值范围, 从而无需开始搜索即可有效地对搜索树剪枝, 甚至在某些情况下将这一步骤作为搜索前的预处理, 无需真正展开搜索即可在预处理中就已经解决问题.

约束传播的核心是 局部相容性: 若我们将变量视为某个图 (Graph) 中的节点 (Vertices), 变量间的约束视为图的边 (Edges), 则若要实现某些节点之间的局部相容性, 就必然导致其余不相容的节点被删除. 下面我们讨论几种局部相容性的定义:

定义 2.1 (节点相容性)

称 某个变量 是 节点相容的, 若其值域中的所有取值都满足它的 一元约束.

显然, 通过执行节点相容, 我们总能消除给定 CSP 问题中的任何一元约束, 进而将任何 $n$ 元约束转换为二元约束. 在随后的内容中, 除非特殊定义, 否则我们默认考虑的求解对象均为二元约束.

2.1 弧相容

定义 2.1.1 (弧相容性)

称 某个变量 是 弧相容的, 若其值域中的所有值都满足它的所有 二元约束.

形式的说, 对变量 $X_i, X_j$, 若对值域 $D_i$ 中的每个数值, 在 $D_j$ 中必存在另一个数值, 满足弧 $(X_i, X_j)$ 的二元约束, 则称 $X_i$ 相对 $X_j$ 为 弧相容 的.

若每个变量对于其他变量都是弧相容的, 则称该网络为 弧相容的.

下面介绍一个最流行的弧相容算法:

算法 2.1.1 (AC-3, AIAA版)

为确保每个变量均为弧相容, AC-3 算法维护一个弧相容集合 (队列):

在初始状态下, 该队列中包含 CSP 问题涉及的所有弧. 算法会依次检查队列中的每一个弧 $(X_i, X_j)$, 并尝试使 $X_i$ 与 $X_j$ 相容. (也就是检查对 $D_i$ 中的每一个值, 是否都能在 $D_j$ 中找到对应的, 弧相容的值).

若执行该步骤后 $D_i$ 不发生变化 (也就是说 $D_i$ 中不存在无法满足 $X_i, X_j$ 相容性的取值), 则处理下一条将要从队列中弹出的弧.

若 $D_i$ 因该步骤的执行而发生变化

(也就是说存在某个变量 $x \in D_i$, 使得无法在 $D_j$ 中找到对应的值满足弧相容性, 由此为了满足 $X_i, X_j$ 的相容性需要将这个值从 $D_i$ 中剔除,因此 $D_i$ 的变化只能是缩小)

, 则需将每个指向 $X_i$ 的弧 $(X_k, X_i)$ 重新插入队列中检验, 因为随着 $D_i$ 的变化, 对于其他弧而言原本某些相容的解 $X_k$ 可能会变得不相容

(如果原来对于 $X_k$ 的某些取值, $x$ 可以满足 $X_i, X_j$ 之间的弧相容性的话, 在上一步从 $D_i$ 中删去 $x$ 后这样的相容性就不成立了)

, 因此必须抓回来重新检测.

若 $D_i$ 变成空集, 则可知该 CSP 问题一定没有相容解 ($X_i$ 和 $X_j$ 之间必然无法相容), 故算法直接返回失败结果, 否则继续检查, 持续缩小变量值域, 直到队列中不再有弧 (确定可以找到对全部变量的一种赋值, 使得约束满足问题中涉及到的所有的弧都相容).

此时, 我们得到的 CSP 问题等价于原问题, 并且我们得到的新问题由于变量值域更小, 所需的求解时间也更短.

伪代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// returns false if an inconsistency is found
// and true otherwise
function boolean AC3(CSP csp) {
    // inputs: `csp`, a binary CSP with components(X, D, C).
    // local variables: `queue`, a queue of arcs, initially all the arcs in `csp`

    while (queue not empty) {
        arc (X_i, X_j) = queue.pop();
        if (REVISE(csp, X_i, X_j)) {
            if (D_i.size() == 0) {
                return false;
            }
            for (node X_k: X_i.Neighbors(X_j)) {
                queue.push(new arc(X_k, X_i));
            }
        }
    }
    return true;
}

// return true iff revised the domain of X_i
function boolean REVISE(csp, X_i, X_j) {
    boolean revised = false;
    for (node x : D_i) {
        if (no_value_in_D_j_allows_(x,y)_to_satisfy_the_constraint_between_X_i_and_X_j) {
            D_i.remove(x);
            revised = true;
        }
    }
    return revised;
}

算法 2.1.2 (AC-3, Slides版)

讲义中所描述的伪代码原理与参考教材中的基本一致, 此处解释伪代码中的数个重要记号:

1. $R_{i,j}$ 记为某个约束集合中的关系, 任何解都需满足这一关系.
2. 伪代码中的函子 $\text{revise(i, j)}$ 描述了从值域 $D_i$ 中删去 $X_i$ 的任何对于弧 $(X_i, X_j)$ 不相容的取值:

\[\begin{aligned}\text{revise(i,j)}:~ D_i :&= D \cap \pi_1(R_{i, j}; D_j) \\ &= \{a \in D_i \vert \exists b \in D_j, \langle a, b\rangle~ \in R_{i, j}\}.\end{aligned}\]

伪代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// returns false if an inconsistency is found
// and true otherwise
function AC3(CSP (X, D, C)) {
    // inputs: `(X, D, C)`, a binary CSP with components.
    // local variables: `Q`, a queue of arcs, initially empty, contains all the arcs in `(X, D, C)` after initialization.

    queue Q = null ;
    for (all i, j, satisfy R_{i,j} in constraint C) {
        Q.push(arc (X_i, X_j));
        Q.push(arc (X_j, X_i));
    }

    // while queue is not empty
    while (Q != null) {
        arc (X_i, X_j) = queue.pop();   // pop off some (X_i,X_j) off Q
        revise(X_i, X_j);
        if (the revise procedure causes a change in D_i) {
            //add to Q all (X_k, X_i) with R_{i,k} in C; i != k, j != k
        }
    }
}

// note the slides version doesn't cut off when it found the CSP is unsatisfiable

// and its revise() method only do the cuts in D_i but does not return any boolean value

// i.e. the pseudo code in the slides are not well implemented...

我们简单讨论一下 AC-3 的时间复杂度.

假设给定 CSP 中包含 $n$ 个变量, 变量值域的大小最大为 $d$, 并且存在 $C$ 个二元约束 (也就是 $C$ 个弧).

对于弧 $(X_k, X_i)$, 由于 $X_i$ 至多有 $d$ 个值可删除, 故每条弧最多只能插入队列 $d$ 次, 故检查一条弧的相容性最多需要 $O(d^2)$ 才能完成.

因此, 在最坏情况下, 算法的时间复杂度为 $O(C \cdot d^2)$.

定义 2.1.2 (有向弧相容性或直接弧相容)

称约束满足问题 $\mathcal{N} = \langle\bar{x}, \bar{D}, C\rangle$ 对于变量顺序 $\bar{x} = x_1, \cdots,x_n$ 为 有向弧相容的 或 直接弧相容, 若对

\[\forall R_{i,j} \in C, ~~ i<j, ~~ \forall a \in D_i\]

存在 $b\in D_j$ 满足 $\langle a, b\rangle ~ \in R_{i, j}.$

2.2 路径相容和 $k-$相容

定义 2.2.1 (路径相容)

称两个变量的集合 ${X_i, X_j}$ 对于第三个变量 $X_m$ 是 相容的, 若对于 ${X_i, X_j}$ 的每一个相容赋值 ${X_i=a, X_j=b}$, 均存在 $X_m$ 的一个合适取值, 使 ${X_i, X_m}$ 和 ${X_m, X_j}$ 均相容.

这样的相容被称为 路径相容, 因我们可以将 $X_m$ 视为从 $X_i$ 到 $X_j$ 的 “路径” 上的一个途经点.

定义 2.2.2 (有向路径相容)

称约束满足问题 $\mathcal{N} = \langle \bar{x}, \bar{D}, C\rangle$ 为 有向路径相容 的, 若对

\[\forall ~ i<j<k, ~~ \forall a_i \in D_i, a_j \in D_j,\]

也就是 $R_{i,j}$ 中的任意一个约束对 $\langle a_i, a_j\rangle$, 存在 $a_k\in D_k$ 满足 $\langle a_i, a_k \rangle ~ \in R_{i, k}$ 且 $\langle a_k, a_j\rangle ~ \in R_{k, j}$.

我们可以使用 $k-$相容 定义更强的传播形式:

定义 2.2.3 ($k-$相容)

对给定 CSP 问题, 若对任何 $k-1$ 个变量的相容赋值, 总能找到第 $k$ 个变量的, 和前 $k-1$ 个变量相容的值, 则该 CSP 就是 $k-$相容的.

在上面两小节中我们分别讨论的 弧相容 和 路径相容 实际上就是 $2-$相容 和 $3-$相容.

定义 2.2.4 (有向 $k-$相容)

称约束满足问题 $\mathcal{N} = \langle \bar{x}, \bar{D}, C\rangle$ 为 有向 $k-$相容的, 若对任何有序的序列 $\bar{y}$ (包含 $k-1$ 个变量), 考虑 长为 $k$ 的有序序列 $\bar{y}x_k$.

任何对 $\bar{y}$ 的相容赋值 $\bar{b}$, 存在一个对该序列中第 $k$ 个变量 $x_k$ 的赋值 $a$, 使得 $\bar{y}x_k = \bar{b}a$ 不与 $C$ 中任何约束冲突, 也就是说它也是相容的.

若 $\mathcal{N}$ 对于任何 $j \leqslant k$ 均为有向 $j-$相容的, 则称其为 强有向 $k-$相容.

2.3 利用强有向 $k-$相容求解约束满足问题

定义 2.2.5 (约束图)

考虑约束问题 $\mathcal{N} = \langle \bar{x}, \bar{D}, C\rangle$, 其约束 $C$ 包含的变量记为 ${x_1, \cdots, x_n}$, 考虑如下的无向图:

\[G = (V, E), ~~ V = \{x_1, \cdots, x_n\}, ~ E = \{(x_i, x_j) ~\vert~ R_{i,j} \in C\}.\]

我们称无向图 $G$ 为约束问题 $\mathcal{N}$ 的 无向约束图.

进一步考虑如下的 有向图:

\[G = (V, E), ~~ V = \{x_1, \cdots, x_n\}, ~ E = \{(x_i, x_j) ~\vert~ i<j, R_{i,j} \in C\}.\]

则称有向图 $H$ 为约束问题 $\mathcal{N}$ 的 有向约束图.

我们同时引入 有向约束图的宽度 的概念:

定义 2.2.6 (有向约束图的宽度)

记有向约束图中 所有节点的父节点数 中的 最大值 为有向约束图的宽度.

显然, 若给定有向约束图的宽度为 $1$, 则该图退化为树.

我们同时有下面的定理:

定理 2.2.1

给定约束图 $G$. 若该约束图为 强有向 $k-$相容 的, 且 $k$ 大于该图的宽度 $w$, 则必存在一个无回溯的, 可以得到解的搜索顺序.

证明
由定义可知, 对给定的约束问题, 存在一个对变量 $x_1, \cdots, x_n$ 的排列 $x_1, \cdots, x_n$, 使有向约束图 $H$ 中任何节点到其父节点的弧数量不超过宽度 $w$.

显然, 若排列中的任一变量 $x_i$ 被赋值, 在该图中可知, 由于该有向约束图为 强 $(w+1)-$约束 的, 且 $x_i$ 最多相容于其他 $w$ 个变量的赋值, 故这个新赋值的变量必与此前所赋值的所有变量相容. $\blacksquare$

我们下面考虑一般的约束图.

定义 2.2.7 (无向约束图的宽度)

与有向约束图不同, 无向约束图的宽度为 所有节点的父节点数 的 最小值.

定义 2.2.8 (环切集)

称某个无向图中全体满足下列性质的边组成的集合为 环切集:

从给定无向图中移除这样的边得到的子图为无圈图.

定理 2.2.2

若 $X$ 为给定约束问题的约束图的环切集, 通过尝试检查 $X$ 中的变量是否相容, 我们就可能得到一个无回溯的约束图.

证明
在之前的讨论中已知, 在检查约束图的某个边 (本质上是一个约束条件) 是否相容时, 若可以找到该边的两个顶点元素的赋值使该约束条件成立, 则我们可以不再考虑这个边, 也就是将其视为被从约束图中删去.

因此, 若我们优先尝试检查环切集中涉及的变量能否与约束条件相容, 在能够找到一组赋值使环切集中所有的边 (也就是某些约束条件) 都能够相容的情况下, 剩余的约束图就是原约束图删去环切集中所有边所得到的无向图.

结合 定理 2.2.1, 我们可知对于任何 无圈的 约束图而言, 若它为 弧相容 的 (也就是 $2-$相容), 则该图必为全局相容的, 由此这样的图是无回溯的. 由此我们就得到了一个无回溯的约束图. $\blacksquare$

2.4 利用树分解求解约束满足问题

我们还可以利用树分解求解约束问题:

定义 2.4.1 (树分解的树宽)

称 树分解的树宽 为给定树分解中节点 (也就是包, Bag) 中包含原约束图节点个数的最大值 $-1$.

需要注意: (Lecture 3, -19:51)

某个图 $G$ (在本章中我们当然只考虑约束满足问题的约束图) 的树分解的树宽 是被该图本身的树宽所限制的:

若图 $G$ 的树宽为 $K$, 则该图的树分解的树宽最少为 $K$.

3. 约束满足问题的回溯算法

在上面的小节中, 我们解释了求解约束满足问题时利用约束使用推理缩小可行解范围的原理和算法, 而在实际情况下很多 CSP 问题无法通过推理求解.

在本节中, 我们讨论在执行推理后的 部分赋值 的回溯搜索算法.

最简单的思路是使用标准的深度优先搜索 (DFS )寻找可行解. 考虑给定的 CSP 中有 $n$ 个值域大小为 $d$ 的变量, 则依次考虑每一层上所有变量的所有赋值, 类推 $n$ 层的话将会生成具 $n! \cdot d^n$ 个叶节点的搜索树, 叶子的数量甚至超过了实际可选的不同完整赋值数 $d^n$, 显然这一方法是不切实际的.

上述的问题建模忽略了 CSP 在给变量赋值时无需考虑赋值顺序的特征, 因此我们在每一层处只需考虑搜索树 选定 节点的 单个 变量. 在这个限制下, 叶节点的个数就回到了 $d^n$, 属于我们可接受的正常范围.

我们在去年的某篇博文中已经详细介绍了 回溯搜索 的基本思想: 每次尝试一种可行的解决方式, 如果当前的解合法的话就尝试下一步, 如果不行的话就退回到上一个可行的方案尝试一个新解, 如此重复这一过程直到最终状态: 找到完整解为止. 约束满足问题的简单回溯算法如下:

我们下面讨论 SELECT-UNASSIGNED-VARIABLE() 中选择新的, 未被赋值的变量的策略.

最简单的策略是按照列表顺序依次选择未赋值变量, 但显然优先选择 剩余可能赋值更少 的变量对搜索树的剪枝效果更好. 这样的选择方法称为 最少剩余值 (MRV) 启发式, 或称为 “最受约束变量” 或 “失败优先” 启发式.

在变量被选定后, 我们还需要决定检验它的取值的顺序. 一种有效的选择方式称为 最少约束值启发式, 这一方法优先选择能够给 “邻居变量留下更多选择” 的值, 也就是说它总是选择给剩余变量赋值留下最大的空间.

对于不同的问题, 选择 具有最少剩余值的变量 可以通过在变量求解的早期有效地对搜索树剪枝, 从而有助于最小化搜索树中的节点数; 而在测试变量值的时候, 优先选择 对其他变量约束最小的值 有助于我们 最快地找到第一个解. 当然, 如果问题需要我们枚举全部解的话, 无论用什么方式选择约束值都是没有意义的.

4. 在搜索过程中执行推理

在上述几节中, 我们介绍了以 AC-3 算法为代表的, 在 搜索前 缩小变量的值域空间从而对搜索树剪枝的方法. 我们还可以 在搜索过程中进行推理 以进一步优化算法的性能: 每次在决定给某个变量赋予某个值时, 我们都可以推理它的临近变量的值域空间.

前向检验 是最简单的推理形式: 只要变量 $X$ 被赋值, 前向检验 就会对这个变量进行弧相容检查: 只要某个未赋值的变量 $Y$ 是通过某个约束和 $X$ 相关联的, 我们就要从 $Y$ 的值域中 删去和 $X$ 不相容的可能取值.

5. 结构化表示约束问题

在处理实际问题时, 我们可以将它分解为多个规模较小的 独立子问题 . 我们可以通过在 约束图中寻找连通子图 来确定独立的子问题: 每个 连通子图 都对应于约束满足问题 $\text{CSP}$ 的一个子问题 $\text{CSP}_i$, 而如果赋值 $S_i$ 是 $\text{CSP}_i$ 的一个解, 则

则为

的一个解.

将规模较大的 CSP 分解为数个彼此独立的子问题并分别解决具有它的重要性. 不妨设每个 $\text{CSP}_i$ 包含总共 $n$ 个变量中的 $c$ 个, 则我们可以将原问题分解为 $\frac{n}{c}$ 个子问题, 而解决每个子问题最多在 遍历每个变量的值域寻找满足约束的解 这一过程中耗费 $d^c$ 步 (我们记这些变量中最大的值域规模为 $d$), 因此总工作量就是

而如果不分解的话, 我们所需要解决的工作量就不再是 $n$ 的线性函数, 而是指数函数

如果一个约束问题可以被直接拆分成数个完全独立的子问题, 对它的求解就会很简单, 但在大多数情况下我们遇到的约束问题并不具备如此美妙的性质. 不过, 当图结构具有某种特性, 比如 当约束图形成一棵树 时, 我们也可以将这样的, 树状结构的 CSP 在它变量个数的线性时间内求解.

在此引入一个新概念:

定义 4.1 (直接弧相容)

设某个约束满足问题的 变量顺序 为

\[X_1, X_2, \cdots, X_n.\]

称该 CSP 为 直接弧相容 的, 当且仅当对所有的 $j > i$, 每个 $X_i, X_j$ 都是 弧相容 的.

求解树结构 CSP 时, 我们首先任选一个变量作为树的根. 然后我们确定一个 变量顺序, 确保 在树中每个变量都出现在父节点之后:

定义 4.1 (拓扑排序)

对于某个树结构 CSP, 满足 在树中每个变量都出现在父节点之后 的变量排序称为 拓扑排序.

如下图所示, $(a)$ 为 约束图, $(b)$ 为一种可能的排序:

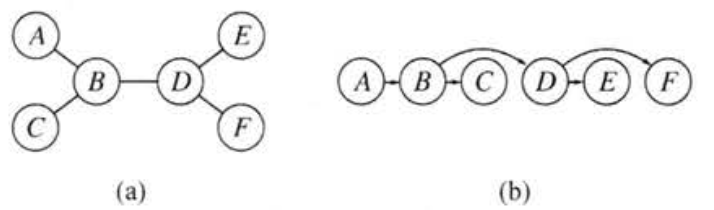
由于具有 $n$ 个节点的树有 $n-1$ 条弧, 因此在 $\text{O}(n)$ 步内可以将它改造为 直接弧相容 的. 在将图改造为直接弧相容的之后, 由于父节点和它的子节点的弧是相容的, 因此无论父节点取什么值, 子节点都有值可选, 也就是说 我们的搜索过程不涉及回溯. 因此, 我们就可以沿着变量列表前进选择任意合适的剩余值.

这样的算法可以表述为下列的伪代码:

如果 CSP 有解, 算法可以在 线性时间内 求解, 反之则会检测到矛盾.

我们下面继续讨论如何将 一般的约束图 化简为 树. 可选的基本方法有两种: 基于删除节点的简化法 和 基于合并节点的简化法.

删除节点简化法 的原理并不是真的从约束满足问题中删去这个节点, 而是 先对部分变量赋值, 从其他变量的值域中 删去与该变量的取值所不相容的值 , 从而相当于在约束图中去掉这个变量代表的节点和所有与之相连的边, 使这个约束图变成一棵树.

基于 “删除” 规则可知, 在剔除掉任何节点和与之相关的约束后, CSP 的每个解都会和它的取值相容. 因此, 用上述的伪代码表示的算法求解剩余的树, 就可以由此得到整个问题的解.

在一般情况下, 往往需要尝试多次才能够为任何要被剔除的变量选择到正确的值. 因此, 我们需要尝试这个变量对应值域中的所有值. 一般算法如下:

1. 从 CSP 的变量中选择子集 $S$, 使约束图在删去 $S$ 对应的节点和所有与这些节点相关的约束 (也就是图的边) 后的剩余子图是一棵树. 称这样的集合 $S$ 为 环割集.

2. 对于满足 $S$ 所有约束的 $S$ 中变量的每个可能的赋值:

   2.1 从 CSP 剩余变量的值域中删去与 $S$ 的赋值不相容的值. 2.2 若去掉 $S$ 后的剩余 CSP 有解, 则将解和对 $S$ 的赋值一并返回.

合并节点简化法 以 约束图的树分解 为基础, 将约束图分解为相关联的子问题. 独立求解这些子问题, 然后将得到的结果合并.

对约束图执行 树分解 需要满足以下三个条件:

1. 原始问题中的每个变量都要至少在一个子问题中出现.
2. 如果两个变量在原问题中通过某个约束相连, 则它们需要至少同时和它们的约束一起出现在一个子问题中.
3. 如果一个变量出现在树中的两个不同的子问题中, 则它必须出现在连接着这两个子问题的路径上的所有子问题里.

前两个条件确保 所有的变量和约束都在分解中有表示, 而第三个所反映的是 任何给定的变量在每个子问题中都必须取值相同.

在执行树分解后, 我们需要 独立求解每个子问题, 若其中任何一个子问题无解, 则 整个问题都无解.

一般来说, 我们可以对一个给定的约束图进行 多种不同的树分解, 而原则是 分解出来的子问题规模越小越好.

从组合数学意义上看, 对某个无向图 $G = (V, E)$ 的树分解记为 $(X, T)$, 其中 $X$ 为由 $V$ 的不同子集 (也称为 “包”): $X_1, X_2, \cdots, X_n$ 组成的集合, $T$ 为树, 且该树的每个节点都由 $X$ 的某个元素表示. 树分解满足:

1. $\bigcup_{i \in [n]} x_i = V$
2. 对图中的每个边 $(v,w)$, 必存在某个同时包含这两个顶点 $v, w$ 的边子集 $X_i$.
3. 所有 包含原图中节点 $v$ 的 树中顶点 都是连通的.

• Previous
  人工智能导论 对抗搜索算法
• Next
  人工智能导论 经典规划