最短路径
本章介引入最短路径的概念并介绍数种用于计算最短路径的算法: 深度优先和 Bellman-Ford 算法, 并讨论单源最短路径问题.
最短路径问题常用于路径规划问题. 如: 给定一个地铁或列车路线图, 设定目标站点和出发站点, 求站点之间的最短路径.
1. 使用广度优先算法查找最短路径
我们首先对 最短路径 给出形式化的定义:
定义 1.1 (最短路径)
称图 $G$ 中以 $s$ 为起始节点, $t$ 为终点的 最短路径 为: 从起始节点到终点, 途径边数最小的路径.
由于广度优先搜索具有 “优先搜索深度更低的同级节点” 的性质, 若我们使用广度优先搜索查找最短路径, 我们总是会优先查找深度更低的节点, 若能生成路径的话也会倾向于生成边数更小的路径, 因此广度优先算法适合解决最短路径问题.
需要注意, 在使用广度优先算法求解最短路径问题时, 我们需要额外存储每个节点的父节点便于在广度优先算法查找不到合适的结果时回溯:

下面讨论基于广度优先的图最短路径查找算法的实现:
它分为 “遍历” 和 “检索” 两个部分:
-
ShortestPaths(s)接受图的某个 没有父节点 的起始节点 $s$ 作为输入, 从 $s$ 开始 完整遍历整个图并将遍历到的每个节点的父节点信息记录在列表 $\pi$ 中.
注意对任何节点而言, 其父节点信息只会被记录一次. 结合广度优先搜索 “优先搜索深度更低的同级节点” 的特性, 这意味着如果某个节点具有多个父节点, 则在这些父节点中只有深度最低, 距离根节点 $s$ 最近的 才会被记录在 $\pi$ 中.
-
GetPath($\pi$, u)接受存储父节点信息的列表 $\pi$ 和目标节点 $u$, 检索 出从 $s$ 到 $u$ 的最短路径.
2. 有权图中的单源最短路径和 Bellman-Ford 算法
我们继续讨论 有权图中的最短路径问题.
首先给出 有权图 的定义:
定义 2.1 (有权图, Weighted Graph)
称每条边都被赋予了对应的 权重 的图为 有权图, 即:
\[G = \langle V, E\rangle, ~~E = \{(u, v) \vert w(u, v) \neq \infty\}\]同时记节点 $u, v$ 之间的路径为 $u\text{p}v$, 此处 $\text{p}$ 表示数量不定的中间节点.
$w$ 为图 $G$ 的 权重矩阵, 它存储 图中每条边的权重.
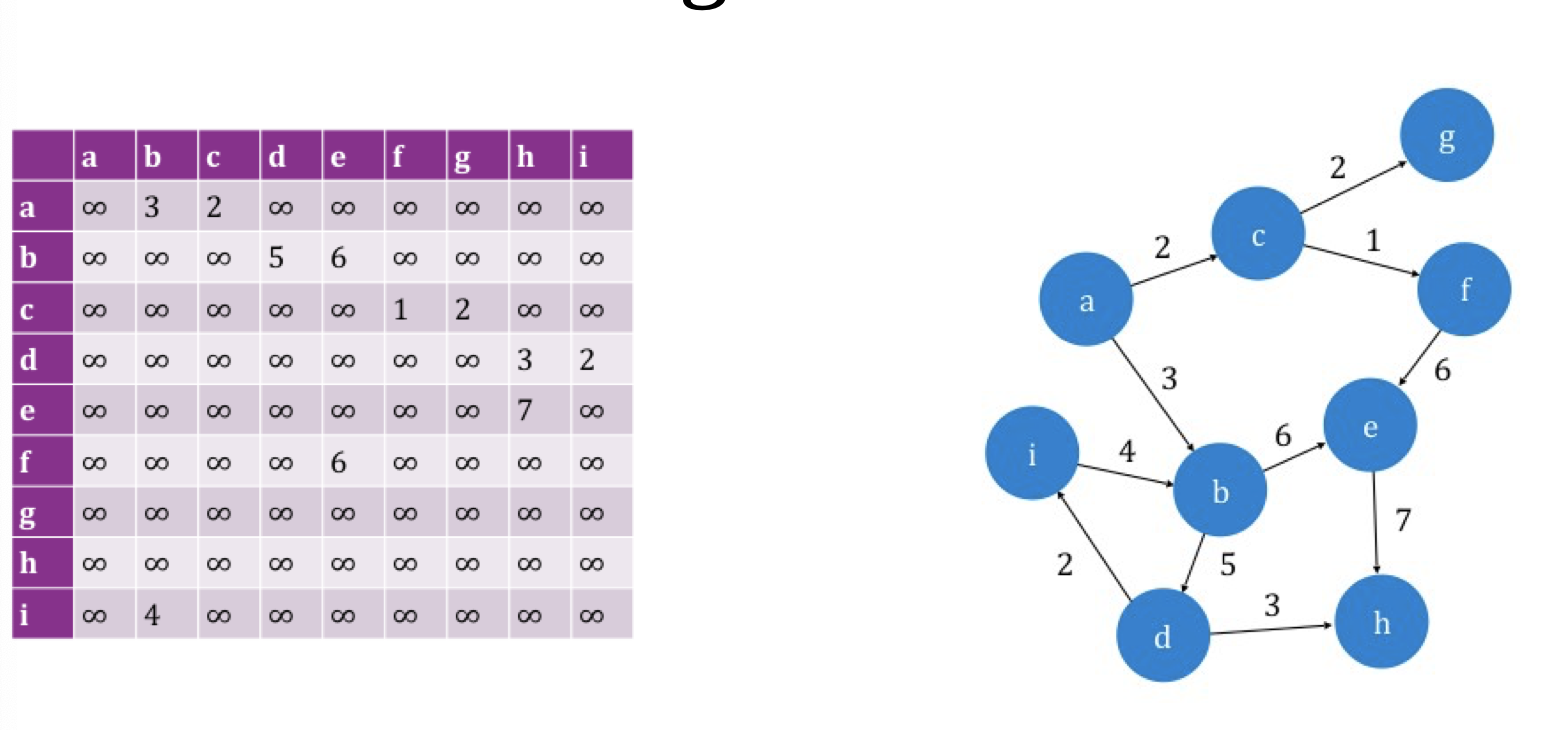
注意:
- 我们可以通过从权重矩阵 $w$ 中查值检测节点之间是否连通: 若 $w(u, v) = \infty$, 说明点 $u$ 和 $v$ 之间不存在边.
- 若 $w(u, v) = d$, 则说明点 $u$ 和 $v$ 之间 存在一条权重为 $d$ 的边.
-
有权图中的路径和常规的有向图中的路径定义一致, 某条路径的权重即为该路径中全部边的权重之和:
\[\vert u_1 \cdots u_n\vert := \sum_{i=1}^{n}w(u_i, u_{i+1})\] - 对应地, 若某条路径的权重为 $\infty$, 说明这样的路径实际上不存在 (不连通).
定义 2.2 (有权图中节点之间的距离)
在有权图中节点 $u, v$ 之间的距离定义为 连通它们的, 权重最小 (最短) 的路径. 即:
\[\delta(u, v) := \text{min}\vert u\text{p}v\vert\]若
\[\delta(u, v) = \infty\]则说明节点 $u, v$ 之间 不存在路径将其连通.
在考虑有权图时, 评判路径长短的标准 不再是路径中边的条数 , 而是 路径中所有边的权重之和, 即: 路径的权重.
下面我们介绍一种用于计算有权图中, 从图的初始节点 $s$ 到任意给定的目标节点 $u$ 之间的 最短路径 的算法: Bellman-Ford 算法.
Bellman-Ford 算法的基本思路是:
-
首先对从起始节点到目标节点的路径权重 $\delta(u)$ 的 上界 $D(u)$ 进行估计:
\[D(s) = 0, ~~ D(u) = \infty, u \neq s\] -
循环地 对每条边进行 松弛 (
Relax) 操作, 使图的节点集 $V$ 中的每个节点 $v$ 到目标节点 $u$ 的距离估计逐渐接近上确界 (即最短路径长):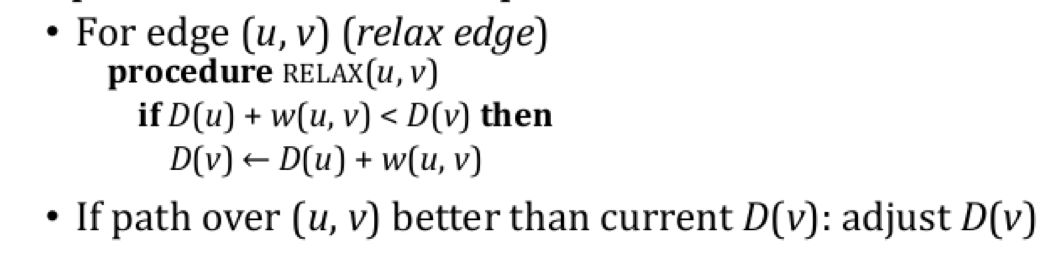
完整的伪代码如下:

注意主方法 BellmanFord(s) 中循环的执行次数: 最多 $\vert V \vert-1$ 次. 这是因为每一次执行内部循环
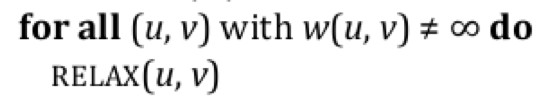
时我们对边的松弛操作实际上都是作用在那些 距起始节点 $s$ 更远的边 (中间隔的边数更多的边) 上的, 首次执行内部循环时所更新的是以 $s$ 为起始节点的边 (和 $s$ 相距 $0$ 条边) 的权重, 第二次更新的是那些和 $s$ 相距 $1$ 条边距离的那些边的权重, 第三次更新的是那些和 $s$ 相距 $2$ 条边距离的那些边的权重… 以此类推.
而考虑最坏情况, 图退化为一条路径, 每次执行内部循环只能更新 $1$ 条边的权重, 此时边数为 $\vert V\vert-1$, 因此需要最多循环 $\vert V\vert-1$ 次才能确保所有的边都被松弛.
在一般情况下, 由于我们既无法预知给定的图是不是一条退化到最坏情况的路径, 也无法控制检查边的顺序, 因此需要对每个节点 (就是检查以该节点为首的所有边, 注意在此我们考虑的是有向图) 都进行检查. 因此我们需要检查的次数也必须是 $\vert V\vert-1$.
实际上, 若在某次执行完对每条边的松弛操作后没有任何一条边的距离估计发生改变, 则说明所有边的估计都达到了上确界, 无需再执行剩下的循环.
3. Bellman-Ford 算法的正确性和复杂度分析
下面讨论 Bellman-Ford 算法的正确性和它的时间复杂度分析.
3.1 算法正确性
在说明 Bellman-Ford 算法的正确性前, 受限引入 循环不变量 的概念:
定义 3.1 (循环不变量, Loop Invarient)
循环不变量 一种有效地证明循环满足某个给定性质的工具, 它在循环中:
- 在初始循环中就已经成立.
- 其正确性在任何一次重复的循环中都被保持.
- 在循环终止后同样保持成立.
下面使用循环不变量说明 Bellman-Ford 算法是能够得出问题的正确解的:
需要检查的声明是:
对于第 $I$ 轮循环,
- 对 从起始节点出发到最远距离为 $I$ 的最短路径 的权重的估计都是精确的.
- 对任意节点 $u \in V$, 都有 $D(u) \geqslant \delta(u).$
考虑第 $0$ 轮循环结束时的情况: 显然估计 $D$ 是精确的. 从起始节点出发到距离最远为 $0$ 条边的节点的最短路径权重只能是 $0$.
考虑第 $i$ 轮循环结束时的情况: 此时不妨假设估计 $D$ 对最远为 $i$ 的路径 (即最多包含 $i$ 条边的路径) 都是精确的.
下面说明在第 $i+1$ 轮循环结束时, 规定的不变量仍然成立:
首先不难看出, 任何最短路径去掉最后的一条边, 即取其 ”前缀“ 得到的仍是最短路径.
不妨考虑路径
\[D(v) = s \rightarrow \mathbf{P} \rightarrow u \rightarrow v\]是一条长为 $i+1$ 的最短路径, 则路径
\[D(u) = s \rightarrow \mathbf{P} \rightarrow u\]也是长为 $i$ 的最短路径. 由归纳假设知 D(u) 也是精确的.
由于第 $i+1$ 轮循环将边 $(u, v)$ 松弛, 因此 $D(v)$ 同样是精确的. $\blacksquare$
由此可知, Bellman-Ford 算法生成的最短路径的估计都是正确的, 也就是说该算法可用于寻找最短路径.
3.2 处理负权圈
我们其次考虑 路径中存在权重为负数的圈 的情况. 在该情况下显然不存在从外界节点到圈中节点的最短路径: 由于构成圈的边权重之和为负, 因此路径在圈中遍历次数越多, 其权重反而被圈的负权重抵消而越来越小, 永不能找到一个权重最小的路径.
因此, 我们不允许最短路径中出现负权圈. 但是注意: 只要图中的负权边不构成任何总权重为负数的图, 这样一类含有负权边的图也适用于 Bellman-Ford 算法!
通过简单修改 Bellman-Ford 算法的伪代码, 我们就可以实现对路径中负权圈存在性的检测:
持续执行循环, 直到任何路径 $s\text{p}u$ 的权重估计 $D(u)$ 都不再发生变化.
若在第 $\vert V\vert$ 次循环中 $D(u)$ 仍然发生变化, 则说明该路径中必包含负权圈.
3.3 时间复杂度
为了确保每条边都被松弛且任何最短路径中均不存在负权圈, 故外层循环需执行
\[\text{max}(\vert V\vert-1, \vert V \vert) = \vert V\vert\]次. 而在每次循环中都需对所有的边进行检查, 故内层循环需执行 $\vert E \vert$ 次.
由于对每条边的松弛操作时间复杂度均为 $O(1)$, 因此 Bellman-Ford 算法总的时间复杂度是 $O(\vert V\vert \vert E\vert)$. $\blacksquare$
