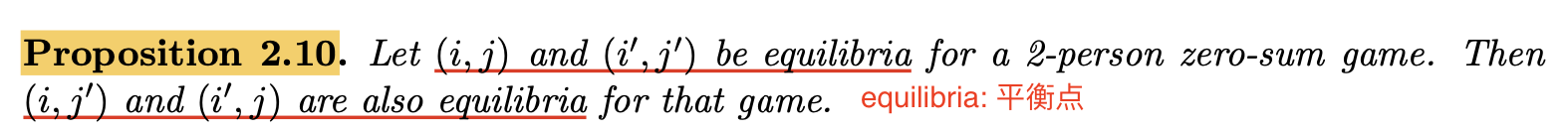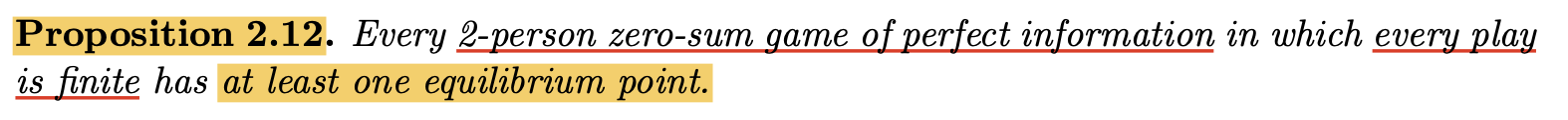2. 均衡问题, 纳什均衡和混合策略
本章主要讨论两个问题: 成功地进行一场博弈意味着什么, 以及 如何寻找一个算得上是 “好” (Desirable) 的策略.
2.1 最优反应 (Best Response)
首先对 “何为成功博弈” 给出定义:
不妨假设一个 双人参与, 零和 且 信息完全 的博弈. 自然, 假设作为博弈的其中一方, 我们会关注 使用什么样的策略会导致己方的收益最大化.
形式上, 我们如此定义 “最好的决策”, 最优反应:
定义 2.1.1 (最优反应 Best Response):
考虑存在 $n$ 个决策者的一个决策. 对决策者 $1$ 而言, 如果存在一个决策 $s_1^*$, 使得它对于任何不同的决策都有:
\[p_1(s_1^*, s_2, \cdots, s_l) \geqslant p_1(s_1, s_2, \cdots, s_l)\]则称其为 最优反应.
显然, 博弈中所有参与的博弈者都可以有属于它们自己的最优反应.
并且, 在 已知自己的所有对手都会做出什么样的决策 的情况下, 我们自然可以选择出对于当前状态的一个最优反应.
考虑更一般的情况, 如果存在某个决策, 使得己方在 对手选择任何策略 的情况下 都是最优反应, 那这样自然是最好的. 但需要注意的是, 绝大多数博弈 中都 不存在 这么美好的情形. 下面给出具备这种性质的博弈需要满足的条件:
命题 2.1.1
若某个博弈者在一个:
- 而人参与
- 零和
- 收益只能是 ${-1, 0, 1}$
的博弈中有一个必胜策略, 则该策略就是该博弈者在这个博弈中关于其他博弈者在 任何情况 下的最优反应.
显然, 很少有博弈能够实际满足上述的所有条件, 具备任何情况下的最优反应. 因此, 从实用的角度我们更关心下面的问题: 如何让博弈 取得均衡.
2.2 纳什均衡 (Nash Equilibrium)
均衡理论 就是研究 那些可以使博弈的所有参与者都处于各自的最优反应 的博弈策略的理论.
我们实际上研究的是博弈中的 均衡点: 它表示 全体博弈参与者各自的策略, 这一组策略对于 每个博弈者 来说都是 在当前状态下 它的 最优反应.
显然, 在均衡点上, 如果任何一个博弈者尝试 单方面地 改变策略, 则影响只会是: 它永不可能得到 比当前更好的回报, 因此每个博弈者都倾向于 (has an incentive) 维持当前的选择.
定义 2.2.1 (纳什均衡点 Nash Equilibrium Point)
称满足上述条件的, 每个博弈参与者的决策组成的元组 $(s_1^, s_2^\cdots, s_l^*)$ 为 纳什均衡点:
我们同时称 $s_i^*$ 为 对其他博弈者的, 互相的最优反应(Simultaneous Best Responses).
需要注意, 如果在均衡点上, 其他所有的决策者都明确它们会做出位于平衡点上的决策, 则剩下的唯一一个决策者为了自身的利益最大化, 能做出的最优决策也就是 同样选择平衡点上的决策 从而 回应其他所有决策者做出的群体选择. 这也是均衡点的一个性质.
这类均衡常被称为 纳什均衡, 我们在本章中不考虑其他更复杂的均衡概念.
下面我们对 双人, 零和, 信息完全 且 不包含概率因素 的某一类博弈给出下列命题:
命题 2.2.1
对 双人, 零和, 信息完全, 不包含概率因素 且 任何博弈主体可能的回报只可能是 ${-1, 0, 1}$ 的博弈, 下列 三种可能情形 中 恰好可能成立一种:
均衡点 概念背后的基本原则是: 它是所有博弈参与者的 “平衡点”: 如果只有其中一个博弈者偏离它,这个博弈者的回报将不可能比平衡点上的决策带来的回报更好, 这是因为在平衡点上, 每个博弈者都在对别人的 集体选择 做出最优反应.
我们下面将讨论在其他不同类型的博弈中是否仍存在均衡点.
如果我们考虑 完全指定的策略 (Fully-Specified Strategy), 则可考虑一个更强的概念:
定义 2.2.2 (子博弈和子博弈均衡点 Sub-Game, Sub-game Equilibrium Point)
称 博弈树中的子树 为 子博弈.
子博弈均衡点是每一个博弈参与者的 完全指定的 选择组成的决策元组, 这个元组是 博弈中每个子博弈 的均衡点:
2.3 非零和博弈中的纳什均衡
我们下面考虑 非零和博弈 中是否存在纳什均衡点, 并讨论非零和博弈可能具有的性质.
非零和博弈中的主要问题是: 它可能存在不止一个纳什均衡点, 但如果使用我们上面提到的原则和定义对博弈双方的最优反应进行计算, 得到的平衡点将是 较差的那个:
如 囚徒困境 中, 如果我们如此分析会得出, 表示为下图的标准形式所示的博弈中, 双方实际选择的平衡点是 (talk, talk) 而非会给双方都带来更好结果的另一个 (don't talk, don't talk).

我们再来看一个 多人囚徒困境 的例子:
考虑 TCP/IP 拥塞控制协议: 所有 TCP 实现都需要支持称为 慢启动 的算法, 其的工作原理如下:
- 初始状态, 将数据包批处理量的大小 (
Batch Size) 约束为 $1$. - 将每次批量发送的数据包数量不断 增加一倍, 直到批量的大小达到预定义的阈值.
- 从到达阈值开始, 每次传输时再将批次大小增加 $1$.
- 当阻塞(在等待接受端发送的
Acknoledgement时超时算作阻塞)时, 将阈值重置为当前 批处理大小的一半 并重新执行第一步中的流程.
其基本思想是: 使批处理的大小 适应网络当前可支持的大小. 由于每个用户都遵循相同的规则, 从而系统会在所有用户之间 平均分配资源, 显然这对集体而言公平的.
然而,对于某个单独的用户来说, 采用比上述慢启动更 “贪婪” 的算法是很诱人的: 比如直接跳回到新的阈值(而不是从批量大小为 $1$ 开始), 这样就可以挤占更多的资源.
而如果每个用户都这样做, 网络带宽将会被榨干, 所有用户都无法以正常的速度发送和接收信息.
这显然是 多人囚徒困境 的情况: 若每个用户都克制追求自身的利益, 达成的结果对群体而言都有利, 每个用户也能获得相对更多的收益, 而在只有极少数人试图作弊时, 它们可以获得比平均水平更好的回报. (事实上, 即使每个用户都使用慢启动算法策略也不会导致均衡)
这显然是不符合任何博弈参与者的最大利益的. 这一问题的基本成因是: 我们在对问题进行建模时 完全排除了博弈者之间沟通与合作的可能.
由此可见:
-
基于平衡点理论对博弈结果进行的计算可能在囚徒困境一般的情况下并不能得到理论上的最优解.
-
在现实中博弈参与者并不完全表现得这般 “自私”.
因此可以使用下列的数种方法缓解纳什均衡理论的缺陷:

2.4 双人零和博弈中纳什均衡的性质
在完全考虑 双人零和博弈 时, 将 达成该博弈的平衡点 视为它的一个 解 的想法是非常有趣的. 下面给出在这种假设下的一系列性质.
首先考虑如何使用最简单的方式找到博弈的平衡点. 我们首先对双人零和博弈的收益情况进行如下图所示的形式化定义:

然后我们有下列的性质:
命题 2.4.1
命题 2.4.2
引理 2.4.1
双人零和博弈中的所有平衡点都会导致 相同的回报.
随后给出 博弈的价值 的定义:
定义 2.4.1 (博弈的价值 Value of the Game)
对双人零和博弈, 它在平衡点上的 (唯一的) 收益被记为该博弈的 价值.
命题 2.4.3
从上面的命题可知: 如果得到了多个平衡点, 则通常可以将它们 组合起来以得到更多的平衡点.
此外, 还可以将 出现在某个平衡点的参与者 $1$ 的任何策略 与 出现在某个平衡点的参与者 $2$ 的任何策略 配对从而 得到另一个均衡点.
因此,为博弈参与者谈论均衡点策略是有意义的. 但是, 这仅在双人零和博弈的情况下才有意义.
故基于 “博弈的价值” 的定义, 有下列的命题:
命题 2.4.4
命题 2.4.5
2.5 混合策略
在博弈中存在 隐藏信息 时, 就需要混合策略:

对于 不存在均衡点 的博弈, 我们可以使用 混合策略, 通过 模拟博弈多次发生 的方式找出所谓的 混合策略.
定义 2.5.1 (混合策略 Mixed Strategy)
博弈者在决策中的 混合策略 就是 它在该博弈中所可以采取的纯策略的概率组合, 一般地表示为 向量 的形式: 向量的每个维度对应某个纯策略, 其值代表在实际博弈中, 选择采用这种纯策略的概率大小.
混合策略用下列所示的方式指示博弈主体如何做出选择: 构造一个性质特殊的随机数生成器, 它以混合策略向量指示的概率生成对应的策略编号. 在开始博弈前, 运行这个随机数生成器, 然后选择它生成的那个编号代表的策略, 在整个博弈过程中都坚持它不变.
显然, 混合策略可以被视为纯策略的一般化: 如果我们想 在任何情况下都一定选择某个特定策略, 就只需要构造某个 特定策略对应的概率为 $1$, 其他任何策略概率为 $0$ 的混合策略向量即可.
混合策略的回报是它每种选择收益关于其概率的 加权和, 换言之它的回报值实际上是各种可能的策略选择下各自回报的 数学期望.
2.5.1 正则形式博弈下的混合策略
对于以正则形式表示的博弈, 考虑一般的情况, 如果双方都采用混合策略并各自的可能策略分别有 $m$ 个和 $n$ 个, 则所有可能的, 实际选择的策略组合就有 $m*n$ 种:

2.5.2 扩展式表述下的混合策略
对于以 扩展式表述 刻画的博弈, 由于此时我们 无从得知所有的可能策略, 因此需要重新定义这种情形下的混合策略.
定义 2.5.2 (博弈的扩展式表述下的混合策略)
在扩展式表述下, 某个决策主体的混合策略被视为 对属于它的信息集中每个决策点分别赋予的概率分布: 我们可能无从得知需要采取什么样的策略才能让决策路径通过信息集中的特定点, 但仍可以刻画这一事件发生的概率.


2.5.3 混合策略中的纳什均衡
混合策略中 均衡点 (Equilibria) 的定义和纯策略中的 相同: 在均衡点上, 给定的混合策略必然相比其他任何策略都是最优反应.
但由于理论上存在无限多个混合策略 (因为概率分布的情况是无限多的), 因此我们无法再像纯策略的情形中那样通过比对有限多个备择策略 (Alternative Strategy) 来确定某个策略是否为最优反应.
在混合策略的情形中, 要确定某个混合策略是否为最优反应, 有以下的引理:

换言之, 要确定混合策略是否为最优反应, 只需将它收益的期望和 所有的纯策略 比对即可.
在多玩家博弈中, 考虑混合策略有以下的结论:

我们最后给出混合策略中纳什均衡的性质:

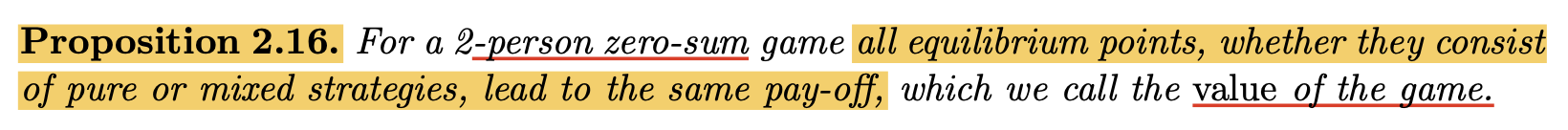
2.6 寻找纳什均衡
下面我们讨论关于 寻找博弈的纳什均衡 的问题.
首先需要考虑 到底需要找到几个均衡点 的问题. 一般地, 对 双人零和博弈 而言, 找到一个均衡点就已经足够; 而对非零和博弈而言, 只找到一个均衡点往往是不够的.
在第一章中, 我们讨论了如何对 决策树剪枝 的方法, 如: 合并子节点完全相同的那些节点 (Symmetry) 从而削减决策树的大小.
对于 只需要找到一个均衡点 的问题, 我们可以将 通过削减决策树, 一步步缩小均衡点存在的范围从而找到均衡点 的这种思想 进一步推广.
定义 2.6.1 (支配, Dominance)
称决策主体 $i$ 的某个策略 $s$ 被它自己的另一个策略 $s’$ 所 支配, 若:
对其他任何决策主体做出的任何选择而言, 决策主体 $i$ 采用策略 $s$ 时的收益总 不超过 另一个策略 $s’$.
换言之, 在 任何情况下, 策略 $s$ 的表现都 始终不如 $s’$. 因此可知, 出于 最大化自身利益 的目的, 决策者 不存在任何选择 $s$ 而不选择 $s’$ 的理由. 因此, 由于 $s$ 永不会被选择, 它就可被从 我们所考虑的可能选择中移除, 就此决策树或决策表的大小就被缩减了.
但是, 即使对于最简单的 双人零和博弈 而言, 单纯基于支配的概念也无法移除足够多的策略.
需要注意, 支配 的概念 不仅局限于纯策略, 在混合策略中同样存在支配的概念. 因此, 我们可以使用下面所述的, 更复杂的方法进一步地找到并移除 更多的被支配策略:
结合之前介绍混合策略时对混合策略中 最优反应 的定义, 给定某个策略, 我们只需要在现存的决策表中 找到任何一个能够将其支配的混合策略, 就可以确定给定的这个策略并非最优反应, 从而就可将其移除.
考虑下面的例子:
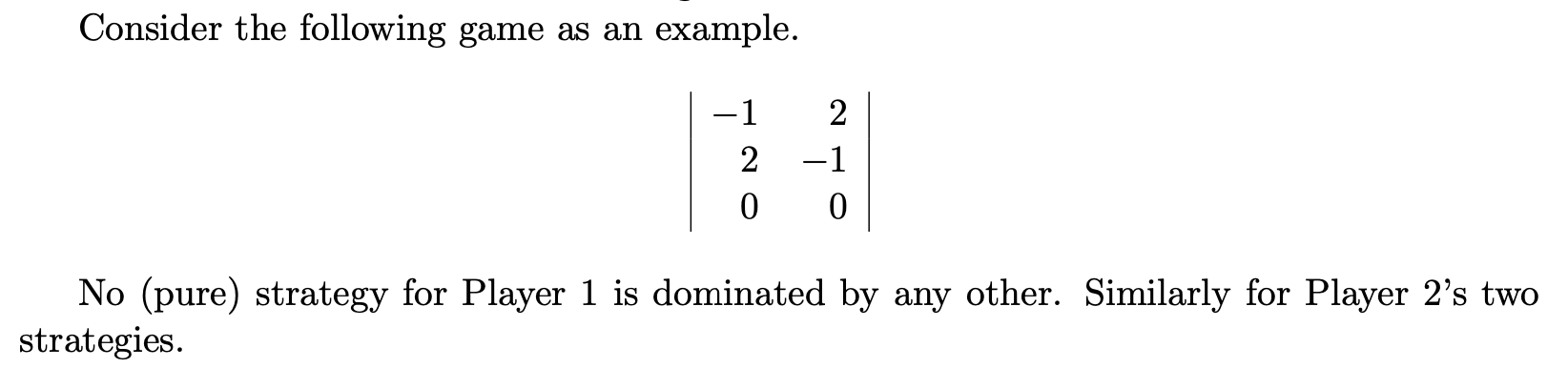
显然对决策者 $1$ (以纵行表示其选择) 和决策者 $2$ (以横列表示其选择) 而言, 都不存在能够被其他任何策略所支配的 纯策略. 因此, 下面需要考虑的问题就是: 对某个决策者而言, 是否存在某个它的策略, 满足该策略被由它的其他策略组成的混合策略所支配, 从而可以被移除 的情况.
我们首先从决策者 $1$ 和决策者 $2$ 中随机选择. 显然因为此处我们考虑的是混合策略, 自然会倾向于选择 可行策略更多 的决策主体, 此处选择 $1$, 它有三种可能的选择.
然后挑选一个最可能被支配的决策. 显然对第一行和第二行而言, 它都在某一列上存在一个当前最大回报 $2$, 而只有第三行对应的决策不是.
因此下面开始考虑: 是否存在某个混合策略
\[(\lambda,1-\lambda, 0)\]支配策略 $3$. 由此可知权重 $\lambda$ 需满足:

然后这里挑选一个在取值范围内的合理数值 $\frac{1}{3}$, 这就是我们可以找到的其中一个 $\lambda$, 它可以使上述的混合策略支配策略 $3$.
由此, 策略 $3$ 就可被安全的从考虑范围内 移除.
显然, 任何经过简化的博弈 $G’$ 的某个混合策略都可以被转化为原来的博弈 $G$ 中的混合策略. 我们有下列的命题: